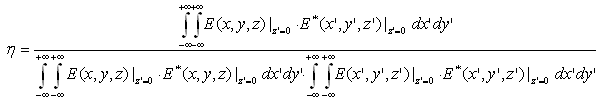|
Coupling-loss characterization of Gaussian beams |
|||||||||||||||||||||||||||||||||
|
Description: The Gaussian Beam is a solution of the Paraxial Helmholtz Equation. Its wavefront normal makes a small angle with z axis, the propagation direction. An expression of the Gaussian Beam complex amplitude is given:
where
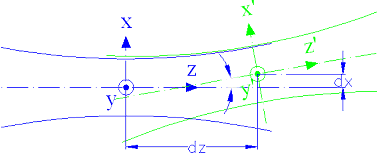
Figure 1 shows two Gaussian Beams with three misalignments, which are beam separation dz, offset dx and angular rotation θ. The coupling efficiency is expressed as:
The coordinate transformation between x, y, z and x ', y ', z ' is given by:
The general formula here provides us the tools to numerically compute the coupling efficiency and its sensitivity due to different misalignments, phase distortion to spot mismatching. Features:
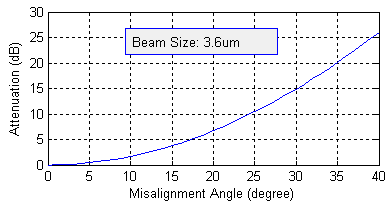
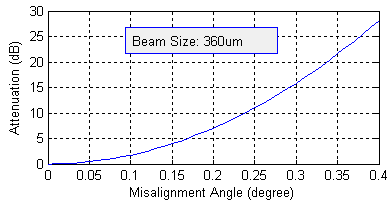
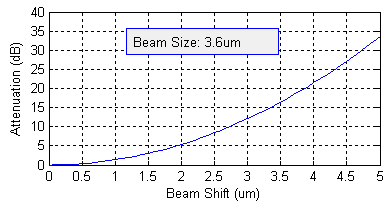
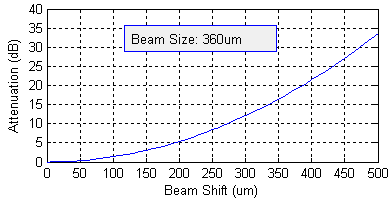
Example: Coupling Efficiency Sensitivity Analysis Figure 2 shows the coupling loss verse offset and angular rotation for two beam sizes of 360 microns diameter at the left and 3.6 microns diameters at the right. The wavelength is 1550nm. The results indicate that a bigger beam size is less sensitive with offset and a smaller beam size is less sensitive with angular rotation, while the product of offset and angular rotation is an almost constant..
Bibliography: [1] Govind P. Agrawal, “Nonlinear Fiber Optics”, Academic Press (1995) [2] Hohn M. Jarem and Partha P. Banerjee, “Computational Methods for Electromagnetic and Optical System”, Marcel Dekker Inc. (2000) [3] Bahaa E.A. Saleh and Malvin Carl Teich, “Fundamentals of Photonics”, John Wiley & Sons Inc. (1991) |
||||||||||||||||||||||||||||||||||
Copyright © 2016 Precision Micro-Optics Inc. All Rights Reserved.

 Services
Services